ADC Resolution & ENOB: LSB, SNR, and Accuracy

Global electronic component supplier ERSAELECTRONICS: Rich inventory for one-stop shopping. Inquire easily, and receive fast, customized solutions and quotes.

Analog to digital converter resolution describes nominal bit depth: N bits produce 2^N output levels and a step size (LSB) of Full-Scale / 2^N. That is not the same as real-world accuracy. ENOB meaning is the “usable bits” once noise and distortion are included; in practice you compute ENOB from SINAD, preferably not just SNR: ENOB = (SINAD − 1.76) / 6.02 (SNR can approximate but excludes harmonics). Start with the next section for quick LSB intuition and 10-/12-/24-bit examples (including why 1024 and 4096 show up). Then see how to measure ENOB with a coherent FFT and how to improve it via reference hygiene, front-end drive, anti-alias filtering, and oversampling. Want a refresher on What is an ADC? Jump to the hub. Need the Hub’s Resolution overview? Open it here.

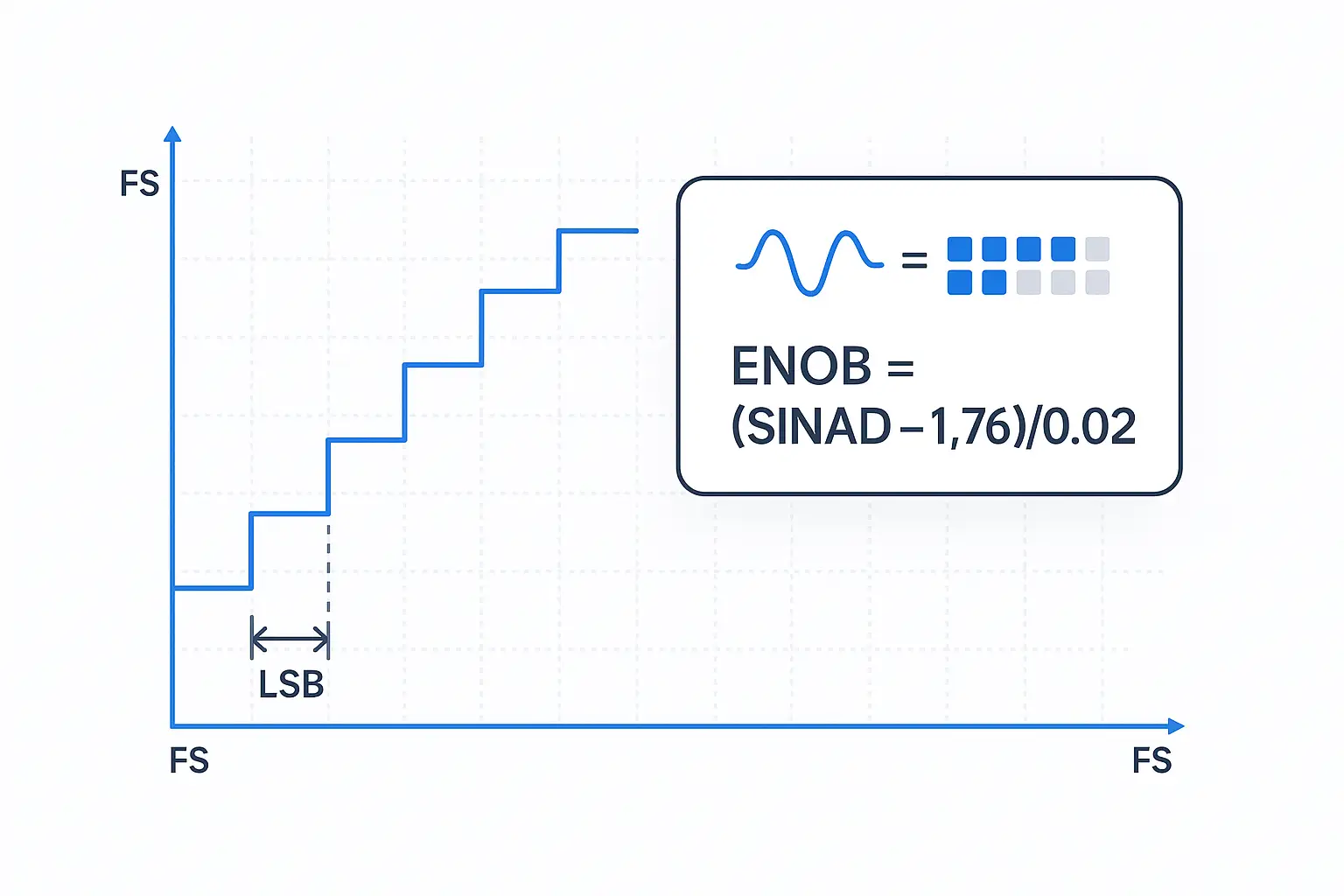
ADC resolution and ENOB at a glance: LSB steps across full-scale and a card suggesting ENOB = (SINAD − 1.76)/6.02, linking adc resolution, enob, and snr. — From nominal steps to usable bits: resolution → ENOB.

Resolution & LSB

This section explains analog to digital converter resolution: how many discrete codes you get and how fine each step (LSB) is—before we account for real-world effects with ENOB in the next sections.

Levels = 2^N · LSB = Full-Scale / 2^N. For single-ended ranges, Full-Scale (FS) is approximately the reference voltage (FS ≈ V_ref); for bipolar ranges, use the full span (FS = V_ref-span, e.g., −V_ref…+V_ref). This is the core ADC resolution formula and the practical voltage resolution formula for step size.

Full-scale range and one LSB step for an ADC, illustrating the voltage resolution formula and step size.

Per-code step as a fraction of full-scale: 10-bit ≈ 0.098% FS (1/1024), 12-bit ≈ 0.024% FS (1/4096), 16-bit ≈ 0.0015% FS (1/65536). These numbers help with “how to select ADC resolution”; real accuracy will be set by ENOB later.

10-bit (3.3 V single-ended) → 2¹⁰ = 1024 levels; LSB ≈ 3.3 / 1024 = 3.22 mV. (also answers “what is 1024 in ADC”)

12-bit (3.3 V single-ended) → 4096 levels; LSB ≈ 3.3 / 4096 = 0.805 mV. (also answers “what is 4096 in ADC” and “what does 12-bit mean”)

24-bit (3.3 V single-ended) → 16,777,216 levels; LSB ≈ 3.3 / 16,777,216 ≈ 0.197 µV (nominal).

How to select ADC resolution (repeatable, 3 steps):

Start from allowable input error → map to LSB with FS / 2^N → get the minimum N.
Check bandwidth/latency budget. If averaging/OSR is allowed, you can trade rate for bits.
Match architecture: low deterministic latency → SAR; highest nominal bits at low bandwidth → delta-sigma (see ADC Types).

Bipolar vs single-ended scaling and divider choices affect FS; verify against sensors’ ranges (Front-End & Vref).
V_ref tolerance and drift can dominate your effective step size; decouple locally and keep grounds short (Front-End & Vref).
Data path width and link rate must carry bits × channels × f_s; budget throughput early (Interfaces later on this page).

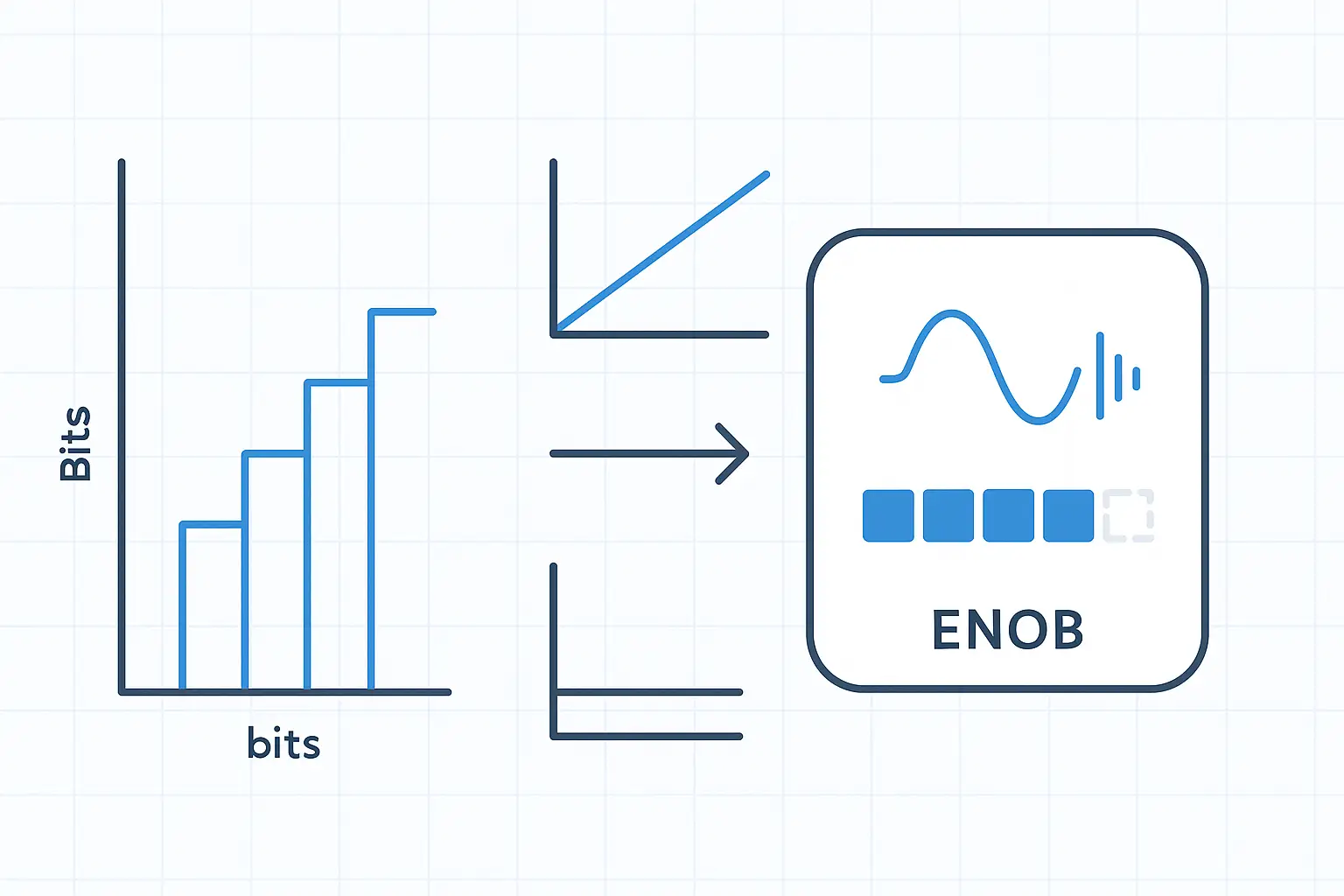
From Resolution → ENOB

Nominal resolution sets step size, but ENOB tells you how many bits you can actually trust in practice.

Ideal SNR for a full-scale sine is approximately 6.02·N + 1.76 dB.

Ideal SNR vs nominal bit depth for a sine input.

SNR excludes harmonics (noise only). THD measures harmonics. SINAD includes noise + distortion. Prefer ENOB from SINAD for realistic, conservative “usable bits”.

ENOB quantifies usable bits: ENOB = (SINAD − 1.76) / 6.02. You can approximate with SNR, but prefer SINAD because it accounts for harmonic distortion. This is the practical ENOB meaning.

Example: if SINAD = 72 dB then ENOB ≈ (72 − 1.76) / 6.02 ≈ 11.7 bits. This is also the starting point for how to calculate ADC accuracy: convert ENOB into equivalent input noise or a fraction of full-scale.

ENOB vs effective resolution: often treated as synonyms. Some vendors define “effective resolution” from RMS noise only (code spread), while ENOB uses SINAD. Always check the datasheet’s definition.

Comparability: ENOB lets you compare real performance across parts and configurations, not just nominal bits.
Frequency sensitivity: at higher input frequencies, jitter-limited SNR pulls ENOB down—fix bandwidth, filtering, and clock quality first.
Whole-chain reality: reference noise, front-end drive/settling, layout, and linearity convert ideal SNR into a lower SINAD (hence fewer usable bits).

What kills ENOB

ENOB falls when noise, distortion, or timing errors dominate. Here is how to improve ADC resolution in practice—by removing the four most common ENOB killers and routing to the right deeper guides.

Reference & Grounds

V_ref noise and ripple couple straight into codes; ground bounce and long return paths turn into visible code jitter.

Action: local decoupling (10 µF ∥ 0.1 µF), partitioned grounds with a single tie, short returns, and Kelvin sensing of the reference node.

Drive & Source Impedance (incl. MUX)

The ADC’s sample capacitor must settle within the aperture; high source impedance or a weak driver raises noise and distortion. Multiplexing reduces effective sample rate and increases code scatter.

Action: buffer or lower source impedance, add RC anti-alias limit, extend acquisition time or slow the MUXed scan as needed.

Clock Jitter & Aliasing

Jitter-limited SNR obeys SNR_jitter ≈ −20·log10(2π·f_in·σ_j): higher input frequency makes ENOB more sensitive to time noise. Unfiltered out-of-band energy folds back and further reduces SINAD.

Action: use a low-phase-noise clock, clean its rails, and set a proper anti-aliasing cutoff/order; keep noisy USB/PLL domains isolated.

Linearity (INL/DNL & Missing Codes)

Nonlinearity converts ideal SNR into lower SINAD, directly cutting ENOB. Missing codes and non-monotonic behavior show up in a code-density histogram.

Action: run a density test, improve symmetry and drive linearity, or choose parts with tighter linearity specs.

Measure ENOB

Use a coherent sine FFT for the primary number, and validate loss sources with code-density and a DC-noise quick check—this covers how to measure ENOB, how to calculate ENOB, and the first step of how to calculate ADC accuracy.

A. Coherent sine FFT (recommended)

Choose tone & amplitude: near full-scale but not clipping (−0.5 to −1 dBFS); avoid front-end saturation.
Coherent sampling: pick integer cycles k and points N so k/N = f_in/f_s. If exact coherence isn’t possible, use a Hann/Blackman window.
Acquire & window: set f_s and record length N (≥65k preferred); apply the chosen window.
Compute FFT & bins: exclude DC and the fundamental; within Nyquist, sum noise + harmonics to get SINAD.
Convert to ENOB: ENOB = (SINAD − 1.76) / 6.02. Prefer SINAD; SNR is only an approximation.

Notes: clean out-of-band junk (anti-alias filter), keep the clock and rails quiet, and make the record long enough; reference/grounds must be stable.

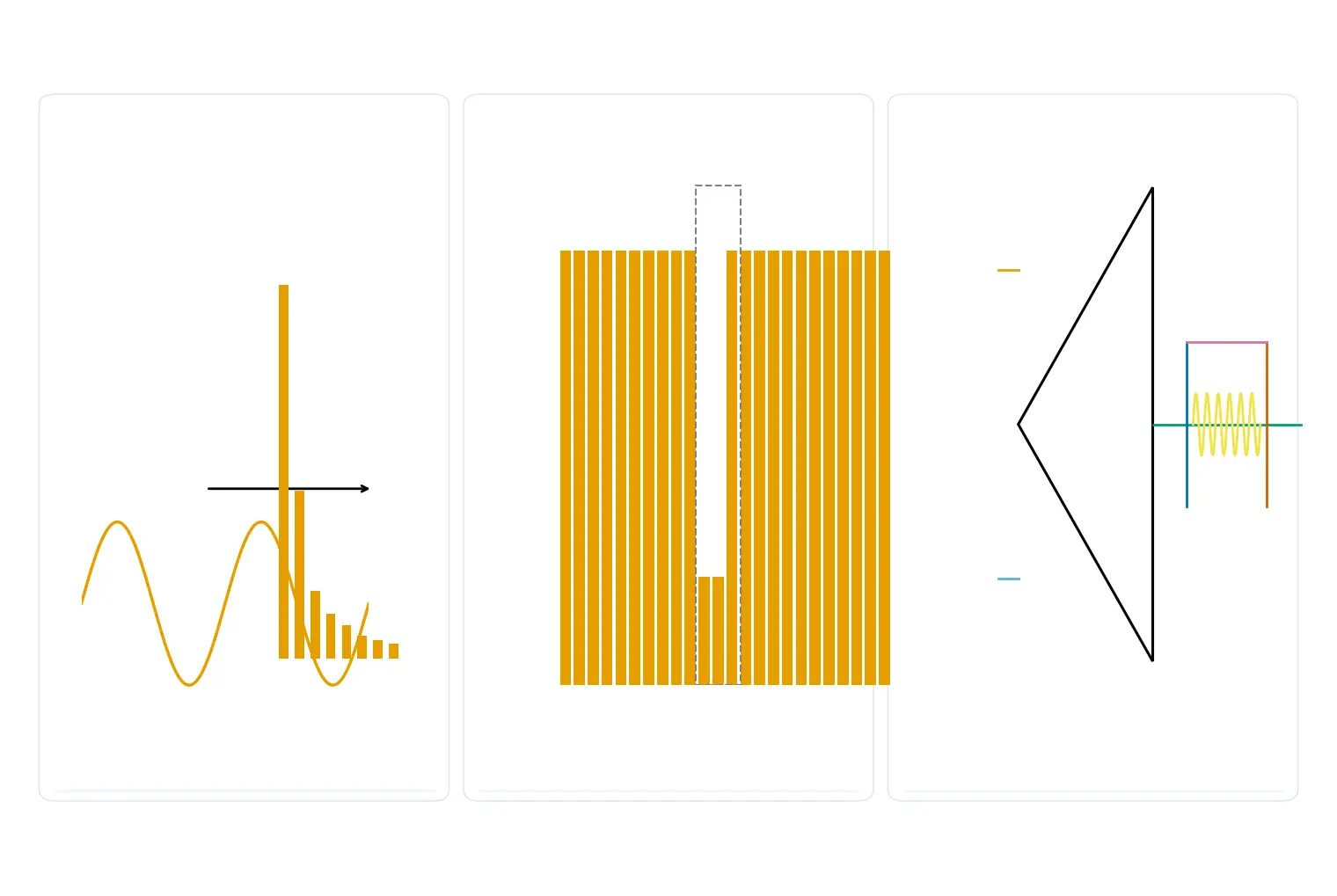
B. Code density (histogram)

Sweep a slow ramp or triangle across the full scale and build a code density histogram. Flatness and holes reveal DNL and missing codes; such nonlinearity lowers SINAD compared with ideal SNR and explains ENOB loss.

C. DC-noise (quick estimate)

Short the input or bias it to mid-scale, record a static code stream, and compute the RMS code width to estimate effective bits. Treat this as a quick health check—the FFT/SINAD method remains the primary reference.

Convert ENOB to equivalent input noise for intuition: V_noise_rms ≈ FS / (2^ENOB · √12) (single-ended FS ≈ V_ref; bipolar use FS = V_ref-span).

Oversampling / OSR & Averaging

If you can spare bandwidth or throughput, oversampling adc and averaging can convert rate into ENOB—up to the limits set by noise correlations.

OSR is defined as OSR = f_s / (2·BW). Under a white, uncorrelated-noise assumption, the effective bit gain follows Δbits ≈ 0.5·log₂(OSR), so 2× ≈ +0.5 bit, 4× ≈ +1 bit, 8× ≈ +1.5 bits, and 16× ≈ +2 bits. This is an upper bound with ideal averaging/filtering.

Oversampling ratio vs. effective bit gain under a white-noise assumption, showing 4× ≈ +1 bit and 16× ≈ +2 bits.

Costs: narrower bandwidth, higher latency, lower throughput, and extra compute/storage for decimation. Limits: correlated noise (reference ripple, supply hum, 1/f, EMI) and tone leakage/aliasing reduce the gain. Delta-sigma ADCs further use noise-shaping beyond the simple 0.5·log₂(OSR) rule (see ADC Types).

If averaging is allowed: pick OSR so that Δbits meets your ENOB target; implement decimation (FIR/IIR) consistent with passband ripple and group delay.
If OSR doesn’t help: first fix V_ref cleanliness, front-end drive/settling, and clock/jitter—averaging cannot remove correlated or deterministic errors.
Verify gains: confirm with the FFT/SINAD path (Section 5) and check there is no alias contamination.

Decision Helpers: How to select ADC resolution

Use this three-step path to pick a starting bit depth, then refine with ENOB and OSR realities. This directly answers how to select ADC resolution for small-batch bring-up.

Step 1 — Allowable error → LSB → starting N

Map your allowable input error to LSB with LSB = FS / 2^N. For single-ended ranges, FS ≈ V_ref; for bipolar, use FS = V_ref-span.

Micro-example: 3.3 V full-scale, allow 2 mV error → 3.3/0.002 ≈ 1650 codes → N ≥ log₂(1650) ≈ 10.7 → start at 12-bit. This is a nominal starting point; real accuracy follows ENOB.

Step 2 — Bandwidth/latency → OSR & averaging?

If bandwidth or latency can be traded, oversample/average to turn rate into effective bits: Δbits ≈ 0.5·log₂(OSR) (2× ≈ +0.5 bit, 4× ≈ +1 bit, 8× ≈ +1.5 bits, 16× ≈ +2 bits). Upper-bound assumes white, uncorrelated noise.

If you can’t slow down, fix correlated errors first (reference cleanliness, front-end drive/settling, clock/jitter); averaging won’t remove them.

Step 3 — System budget → pick architecture

Check V_ref purity, input drive/source impedance, clock/jitter, channels × f_s throughput, package, and power.
SAR: low, deterministic latency; easy multi-channel; broad availability.
Delta-Sigma: highest nominal bits at low bandwidth; accepts group delay.
Pipeline: high-speed DAQ/IF/imaging; Flash for ultra-low latency triggers.

Quick Table

Bits

Ideal SNR (dB)

Levels (2^N)

LSB @ 3.3 V

Bits

Ideal SNR (dB)

61.96

Levels (2^N)

1,024

LSB @ 3.3 V

3.223 mV

Bits

Ideal SNR (dB)

74.00

Levels (2^N)

4,096

LSB @ 3.3 V

0.806 mV

Bits

Ideal SNR (dB)

86.04

Levels (2^N)

16,384

LSB @ 3.3 V

0.201 mV

Bits

Ideal SNR (dB)

98.08

Levels (2^N)

65,536

LSB @ 3.3 V

0.050 mV

Bits

Ideal SNR (dB)

110.12

Levels (2^N)

262,144

LSB @ 3.3 V

0.0126 mV

Note: Ideal SNR is for a full-scale sine; actual accuracy follows ENOB.

FAQ

What is ADC resolution and step size?

ADC resolution is nominal bit depth; step size is the smallest code increment. Use the voltage resolution formula LSB = FS / 2^N (single-ended FS≈Vref; bipolar uses full-span). Resolution sets the ceiling on detail—actual accuracy depends on ENOB after noise and distortion. Read more → Resolution & LSB.

What is the resolution of a 10-bit ADC? / What is 1024 in ADC?

10-bit means 2¹⁰ = 1024 discrete levels. With a 3.3 V single-ended range, the nominal step is LSB ≈ 3.3/1024 = 3.22 mV. This is nominal resolution; usable accuracy depends on ENOB, which includes noise and distortion. Read more → 10-bit example.

What is 12-bit resolution / What is 4096 in ADC?

12-bit produces 4096 levels. At 3.3 V single-ended, the nominal step is LSB ≈ 3.3/4096 = 0.805 mV. “12-bit” names code depth; effective accuracy is set by ENOB from measured SINAD. Read more → 12-bit example.

What is the resolution of a 24-bit ADC?

24-bit gives 16,777,216 nominal levels. With 3.3 V single-ended, the nominal step is ~0.197 µV. That’s a ceiling: real devices deliver fewer usable bits because ENOB falls with noise, distortion, jitter, and bandwidth. Read more → 24-bit note.

How accurate is a 12-bit ADC?

Accuracy follows ENOB, not nominal bits. Measure SINAD with a coherent FFT, then compute ENOB = (SINAD − 1.76)/6.02. Low reference noise, stable drive/settling, and low-jitter clocks help ENOB approach nominal. Read more → Why ENOB sets accuracy.

How do you calculate ENOB?

Prefer SINAD over SNR because it includes harmonics. After measuring SINAD from your FFT, use ENOB = (SINAD − 1.76)/6.02. This gives realistic “usable bits” for your setup and bandwidth. Read more → Measure ENOB.

Why is ENOB important? / What is SNR vs THD in ADC?

ENOB compares real performance across parts and settings, including frequency-sensitive limits like jitter. SNR excludes harmonics; THD measures harmonics only; SINAD includes both and is preferred for ENOB. Read more → SNR/THD/SINAD mini-card.

How to improve ADC resolution / increase ENOB?

First remove correlated errors: clean Vref and grounds, buffer the input so the sample cap settles, and control aliasing and clock jitter. If bandwidth allows, use oversampling/averaging to trade rate for bits. Read more → What kills ENOB.

Send your specs or BOM and get three safe options in 48 hours—each with indicative lead time, price range, and basic front-end/Vref notes.

Submit your BOM (48h) See IC selection guide

Cut-Tape / Partial Reel / AEC-Q available.